To widen the range of application
and deployment of robots, both
in
research and in industrial con-
texts, we need to develop more powerful
and flexible robotic
systems
exhibiting
higher degrees of autonomy and able to
sense, plan, and operate in
unstructured
environments.
For that, the robot must be
able to interact coherently with its world,
both by being able to
recover robust
and
useful spatial descriptions of its surround-
ings using sensory information and
by
efficiently
utilizing these descriptions in
appropriate short-term and long-term plan-
ning and decision-making
activities.
This article reviews a new approach to
robot perception and world modeling
that
uses a
probabilistic tesselated representa-
tion of spatial information called the occu-
pancygrid.' The occupancy grid is a
multi-
dimensional random field that maintains
stochastic estimates of the occupancy state
of the
cells
in a spatial lattice. To construct
a sensor-derived map of the robot’s world,
the cell state
estimates are
obtained by
interpreting the incoming range readings
using probabilistic sensor models.
Baye-
sian
estimation procedures allow the
incre-
mental updating of the occupancy grid
using readings taken from
several sensors
over multiple points
of view.
The occupancy grid framework repre-
sents a fundamental departure from
traditional
approaches to robot perception and
spatial reasoning. By utilizing probabilis-
tic
sensor models and representation
schemes, this approach supports the devel-
opment of agile and
robust
sensor interpre-
tation mechanisms, incremental discovery
procedures, explicit handling of
uncer-
tainty,
multisensor composition of infor-
mation, and spatial reasoning tasks within
an integrated
framework.
The following sections give an over-
view of the occupancy grid framework
and
illustrate
its application to a number of
problems in the mobile robot domain, in-
cluding range-based mapping,
multiple-
sensor integration, path planning and navi-
gation, handling of sensor position
uncer-
tainty
due to robot motion, and related
tasks. I contrast the occupancy grid frame-
work to geometric
approaches to
sensor
interpretation and suggest that a number of
robotic tasks can be performed directly on
the
occupancy grid representation. I con-
clude with an overview of further research.
Spatial sensing and
modeling for
robot
perception
One of the long-term goals of the re-
search discussed in this article has been
the
development of robust mapping and navi-
gation systems for mobile robots operating
in and
exploring
unstructured and un-
known environments.
Such scenarios occur in a variety of
contexts. Robot rovers being developed
for
planetary
and space exploration, or
autonomous submersibles devoted to sub-
marine prospecting and surveying,
have
to
deal with unexpected circumstances and
require the ability to handle complex and
rough
environments
with little or no prior
knowledge of the terrain. While planetary
rovers may take advantage of
terrain maps
obtained from orbiting surveyors for
global
planning strategies, these will be of
limited resolution and not useful for de-
tailed path planning
and
navigation.
On the other hand, mobile robots devel-
oped for factory automation purposes or
for
operation in hazardous mining environ-
ments or nuclear facilities generally can be
expected to
operate in
more constrained
situations and to have access to precom-
piled maps derived from plant
blueprints.
However, such maps may become out-
dated. Additionally, over the long dis-
tances
traversed
by autonomous vehicles,
inertial or dead-reckoning navigation
schemes may accumulate substantial
posi-
tional errors. This makes it difficult for the
robot to position itself in precompiled
world
models, to register sensor informa-
tion to an absolute frame of reference, or to
construct global
maps that
are precise in
Cartesian coordinates.
These considerations lead to some fun-
damental requirements for mobile
robots.
Autonomous vehicles must rely heavily on
information recovered from sensor data
and must be
able
to operate without pre-
compiled maps. Sensor views obtained
from multiple sensors and different
loca-
tions have to be integrated into a unified
and consistent world model, and sensor
uncertainty
and
errors have to be handled.
Precompiled maps, when available, should
be used to complement
sensor-derived
maps. Finally, the positional drift of the
sensors due to the robot motion has to
be
taken
into account in the mapping and
navigation procedures.
Traditional approaches to sensor inter-
pretation for robot perception have
largely
relied on the recovery and manipulation of
geometric world models.1 Low-level
sens-
ing processes extract geometric features
such as line segments or surface patches
from the sensor
data, while high-level
sensing processes use symbolic models,
geometric templates, and prior
heuristic
assumptions about the robot’s environ-
ment to constrain the sensor interpretation
process. The
resulting geometric world
models serve as the underlying representa-
tion for other robotic tasks, such as
ob-
stacle avoidance, path planning and navi-
gation, or planning of grasping and assem-
bly
operations.
These approaches, which as an ensemble
characterize what we refer to as the geo-
metric paradigm in robot perception,
have
several shortcomings.1 Generally speak-
ing, the geometric paradigm leads to sparse
and
brittle world models; it requires early
decisions in the interpretation of the sensor
data for the
instantiation of specific model
primitives; it does not provide adequate
mechanisms for handling sensor
uncer-
tainty and errors; and it relies heavily on
the adequacy of the precompiled world
models and the
heuristic assumptions used,
introducing strong domain-specific de-
pendencies. Better descriptions of
the
robot’s environment are derived primarily
from the application of finer tuned prior
models and
additional constraints to the
available sensor data, rather than from
strategies based on additional
sensing.
Because of these shortcomings, the
geometric paradigm implicitly creates a
wide gap between two informational layers:
the layer that corresponds to the impre-
cise and limited information
actually pro-
vided by the sensor data, and the layer of
abstract geometric and symbolic world
models
operated on by the sensing and
world modeling processes. Consequently,
geometric approaches to robot
perception
may be useful in highly structured do-
mains, but have limited applicability in
more complex
scenarios, such as those
posed by mobile robots.
Occupancy grids
The occupancy grid framework ad-
dresses the requirements and concerns
outlined above
through the development
of spatial robot perception and reasoning
mechanisms that employ
probabilistic
sensor interpretation models and random
field representation schemes. In so doing,
it
supports robust mapping and navigation
strategies and allows a variety of robotic
tasks to be addressed
through operations
performed directly on the occupancy grid
representation.
This section provides a brief overview
of the occupancy grid formulation, while
the
following sections illustrate the appli-
cation of occupancy grids to the mobile
robot mapping and
navigation domain. The
actual derivation of the probabilistic esti-
mation models used is beyond the scope
of
this article and can be found elsewhere,12
as can more detailed discussions of
the
experimental work.14
Occupancy grid representation. The
occupancy grid representation employs a
multidimensional (typically 2D or
3D)
tesselation of space into cells, where each
cell stores a probabilistic estimate of its
state.
Formally, an occupancy field O(x) is
a discrete-state stochastic process defined
over
a set of continuous spatial coordinates
x= (x1,x2,..., xn), while the occupancy grid
is a lattice
process, defined over a discrete
spatial lattice. The state variable s5(C) asso-
ciated with a cell
C of the occupancy grid
is
defined as a discrete random variable
with two states, occupied and empty, de-
noted OCC and EMP. Consequently,
the
occupancy grid corresponds to a discrete-
state binary random field.5 Since the
cell
states are exclusive and exhaustive, P[s(C)
= OCC] + P[s(C) = EMP] = 1. More gen-
eral models are
possible by using a random
vector and encoding multiple properties in
the cell state. I refer to these
representa-
tions as inference
grids.1 This article dis-
cusses the estimation of a single
property,
the occupancy state of each cell.
Estimating the occupancy grid. Since
a
robot can only obtain information about
its environment indirectly, through its
sensors, the recovery of a
spatial world
model from sensor data is best modeled as
an estimation theory problem. The specific
steps
involved in estimating the occupancy
grid from sensor readings are sketched out
in
Figure 1.
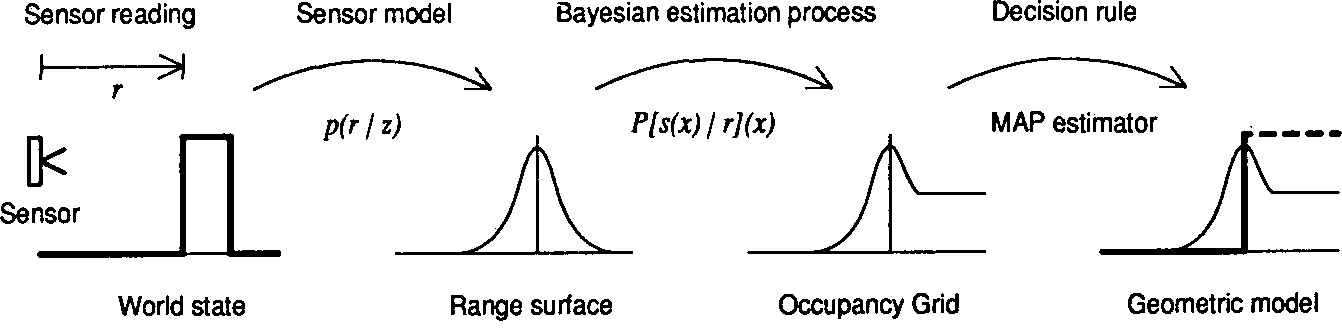
Figure 1. Estimating the occupancy grid from sensor data.
To interpret the range data obtained
from a given sensing device, we use a sto-
chastic
sensor model defined by a proba-
bility density function of the form p(r | z),
which relates the reading r to the true
parameter space range value
z. This den-
sity function is subsequently used in a
Bayesian estimation procedure to deter-
mine the
occupancy grid cell state proba-
bilities. Finally, we can obtain a determin-
istic world model, using
optimal estima-
tors such as the maximum a posteriori
(MAP) decision rule to assign discrete
states to
the cells, labeling them occupied,
empty, or unknown. We emphasize, how-
ever, that many robotic tasks can
operate
directly on the occupancy grid representa-
tion.
In the discussion below, the occupancy
grid is modeled as a Markov random
field
(MRF)5 of order 0, so the individual cell
states can be estimated as independent
random
variables. We can employ compu-
tationally more expensive estimation pro-
cedures for higher order
MRFs.
To allow the incremental composition
of sensory information, we use the sequen-
tial
updating formulation of Bayes’ theo-
rem to determine the cell occupancy proba-
bilities.1 Given
a current estimate of the
state of a cell C, P[s(Ci) = OCC | {r}|t],
based on observations {r}=
(r1,...,
rt) and
given a new observation rt+1 the improved
estimate is given by
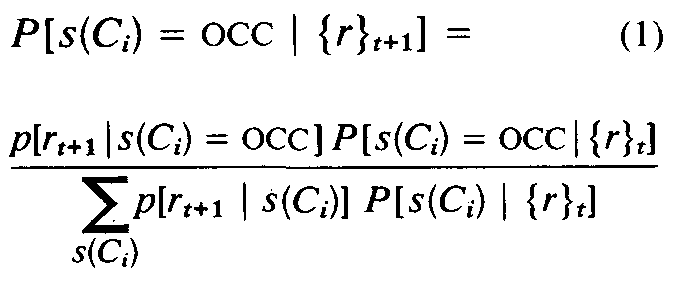
In this recursive formulation, the previ-
ous estimate of the cell state, P[s(Ci) =
OCC | {r}t], serves as the prior and is
obtained directly from the occupancy grid.
The new cell state estimate P[s(Ci) = OCC
| {r}t+1] is subsequently stored again in the
map. For the initial prior cell state proba-
bility estimates, we use maximum entropy
priors.6 Obtaining the p[r | s(Ci)] distribu-
tions from the sensor model p(r | z) is done
using Kolmogoroff’s theorem.7 We can
derive closed form solutions of these equa-
tions for certain sensor models andcom-
pute numerical solutions in other cases.
To illustrate the approach, Figure 2
shows the occupancy profile derived for
the case of a one-dimensional ideal range
sensor, characterized by p(r | z) = δ(r-z).
Given a range reading r, the corresponding
cell has occupancy probability 1. The pre-
ceding cells are empty and have occupancy
probability 0. The succeeding cells have
not been observed and are therefore un-
known, so the occupancy probability is
0.5.
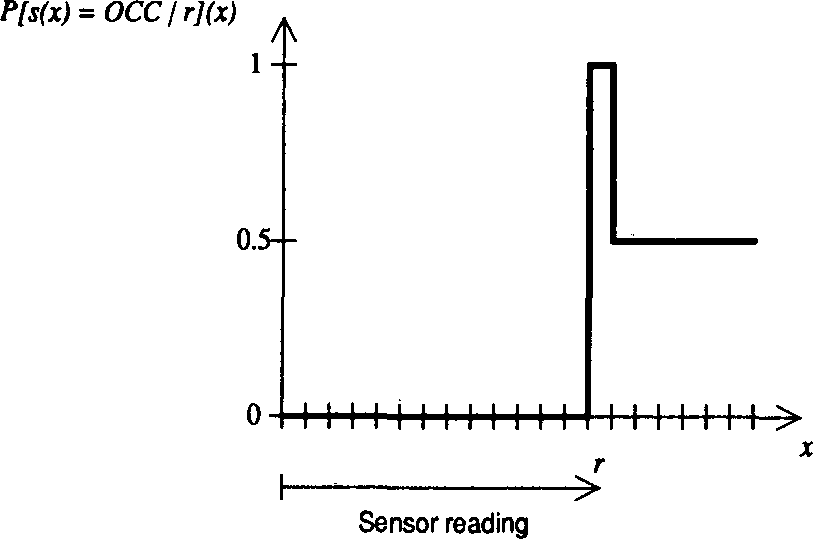
Figure 2. Occupancy probability profile for an ideal sensor.
A sequence of occupancy profiles ob-
tained from a one-dimensional Gaussian
range sensor appears in Figure 3. The sen-
sor model
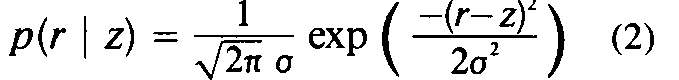
is shown superimposed (dashed line). Sev-
eral successive updates of the occupancy
probabilities are plotted, with the sensor
positioned at x=0.0 and r=2.0. The grid
was initialized to P[s(x) = OCC](x) = 0.5.
The sequence of occupancy profiles shows
that the occupancy grid converges towards
the behavior of the ideal sensor.
Finally, a two-dimensional occupancy
grid generated from a single sonar range
reading is shown in Figure 4. The sonar
sensor is modeled with Gaussian uncer-
tainty in both range and angle. The sensor
probability density function is given by
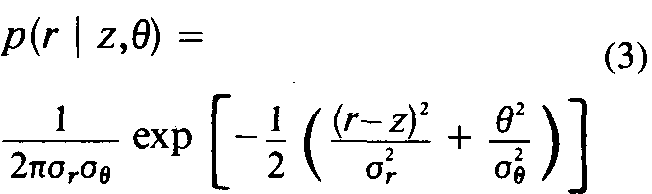
The occupancy profile shown corre-
sponds to a range measurement taken by a
sonar sensor positioned at the upper left
and pointing to the lower right. The hori-
zontal surface corresponds to the unknown
level.
Sensor integration. To increase the
capabilities and performance of robotic
systems in general requires a variety of
sensing devices to support the various
tasks to be performed. Since different
sensor types have different operational
characteristics and failure modes, they can
in principle complement each other. This
is particularly important for mobile robots,
where multiple sensor systems can be used
to generate improved world models and
provide higher levels of safety and fault
tolerance.
Within the occupancy grid framework,
sensor integration can be performed using
a formula similar to Equation 1 to combine
the estimates provided by different sen-
sors.1,2 For two sensors S1 and S2, this
requires using the corresponding sensor
models p1(r|z) and p2(r | z). As a result, the
same occupancy grid can be updated by
multiple sensors operating independently.
A different estimation problem occurs
when separate occupancy grids are main-
tained for each sensor system and the inte-
gration of these sensor maps is performed
at a later stage by composing the corre-
sponding cell probabilities. This scenario
requires the combination of probabilistic
evidence from multiple sources, which can
be addressed using an estimation method
known as the independent opinion pool.6
This method involves summing the evi-
dence for each cell state and performing
the appropriate normalization.
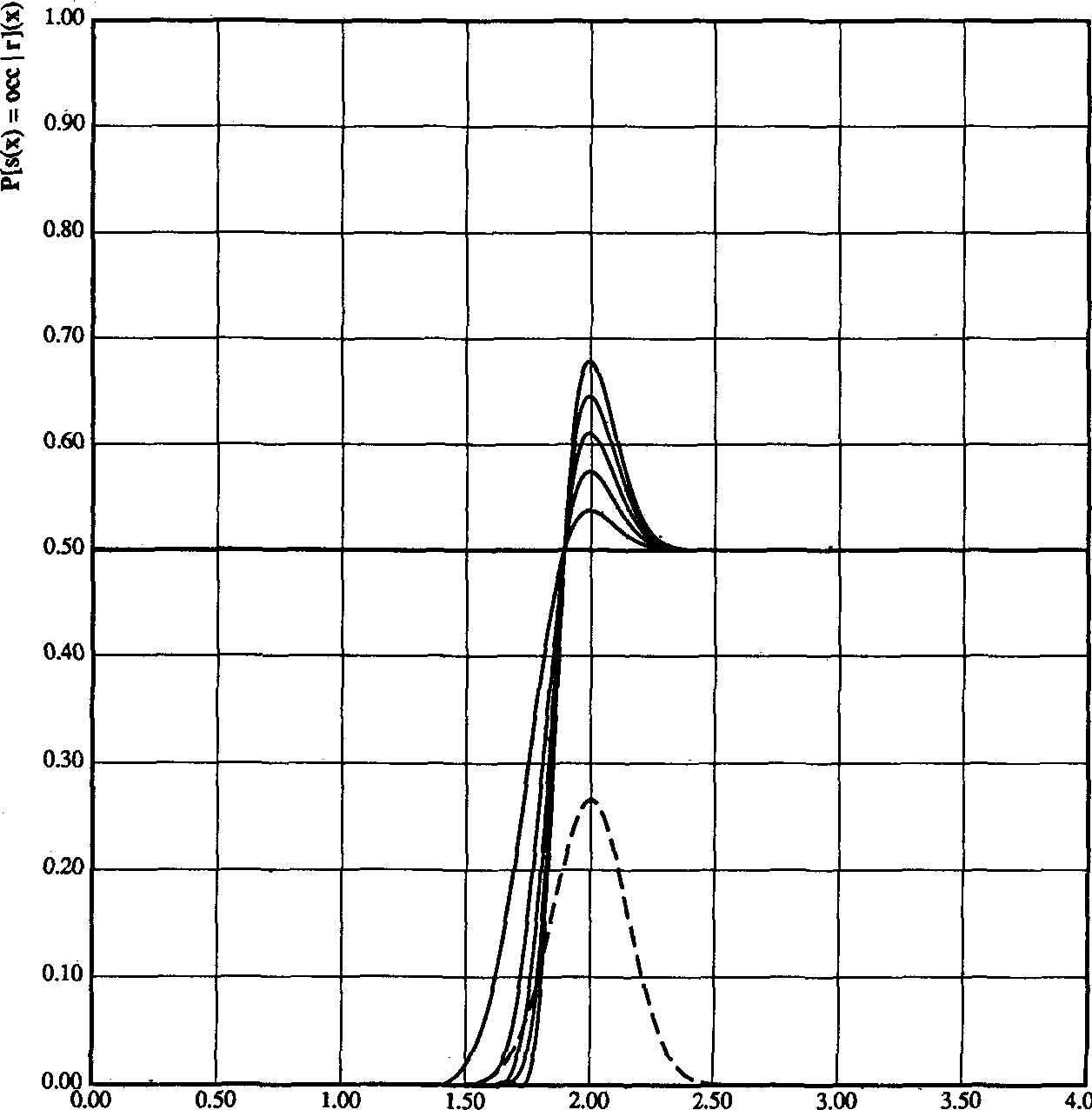
Figure 3. Occupancy probability profiles for a Gaussian sensor.
Incorporation of user-provided maps.
Throughout this article we are mainly
concerned with scenarios where the robot
operates in unknown environments, so no
prior maps can be used. As already men-
tioned, however, in some situations such
knowledge is available and can be repre-
sented using geometric and symbolic
models.8
The Occupancy grid framework incor-
porates information from such high-level
precompiled maps using the same method-
ology outlined in the previous sections. To
provide a common representation, the
geometric models are scan-converted into
an occupancy grid, with occupied and
empty areas assigned appropriate proba-
bilities. These precompiled maps can sub-
sequently be used as priors or can simply
be treated as another source of information
to be integrated with sensor-derived maps.
Decision making. For certain applica-
tions, it may be necessary to assign spe-
cific states to the cells of the occupancy
grid. An optimal estimate of the state of a
cell is given by the maximum a posteriori
(MAP) decision rule7: a cell C is occupied
if P[s(C) = OCC] > P[s(C) = EMP], empty
if P[s(C) = OCC] < P[s(C) = EMP], and
unknown if P[s(C) = OCC] = P[s(C) =
EMP].

Figure 4. Occupancy grid for a two-dimensional Gaussian sensor.
We could use other decision criteria,
such as minimum-cost estimates. Depend-
ing on the specific context, it may also be
useful to define an unknown band, as
opposed to a single thresholding value.
However, many robotic tasks can be per-
formed directly on the occupancy grid
precluding the need to make discrete
choices concerning the state of individual
cells. In path planning, for example, we
can compute the cost of a path in terms of
a risk factor directly related to the corre-
sponding cell probabilities.'-3
Characteristics of the occupancy grid
approach. From the foregoing discussion,
several aspects of the occupancy grid
framework become evident. I have stressed
the use of probabilistic sensor models to
perform sensor interpretation and handle
sensor uncertainty, and the use of probabil-
istic estimation procedures to update the
occupancy grid. Consequently, no precom-
piled geometric models and no runtime
segmentation decisions are necessary.
Additionally, the use of a decision-theo-
retic framework makes possible state-
ments about the optimality of the esti-
mates.
Further note that the occupancy grid
itself provides a stochastic spatial world
model. The random field explicitly en-
codes both the spatial information and the
associated uncertainty, and does not re-
quire discrete choices. It is possible to
derive deterministic voxel models or
higher-level geometric representations
from the occupancy grid; however, the
suitability of a representation is directly
related to how well it describes its subject
and how easily relevant information can be
extracted from it. From this point of view,
I argue that a number of robotic tasks can
be efficiently addressed within the occu-
pancy grid framework.1
This approach also has some specific
implications. Due to the intrinsic limita-
tions of sensor systems, spatial sensor
interpretation is fundamentally an under-
constrained problem. Within the occu-
pancy grid framework, we achieve disam-
biguation of the sensor data and recovery
of better world models primarily through
strategies that emphasize additional sens-
ing, rather than through the use of finer
tuned heuristics or additional assumptions
about the robot’s environment. Instead of
relying on a small set of observations to
generate a world model, we compose in-
formation from multiple sensor readings
taken from different viewpoints to esti-
mate and improve the sensor-derived oc-
cupancy grids. This leads naturally to an
emphasis on a high sensing-to-computation
ratio and on the development of im-
proved sensor models and active sensing
strategies.
Figure 5 provides a contrast between
some of the emphases in the occupancy
grid approach and in the geometric para-
digm, outlined earlier.
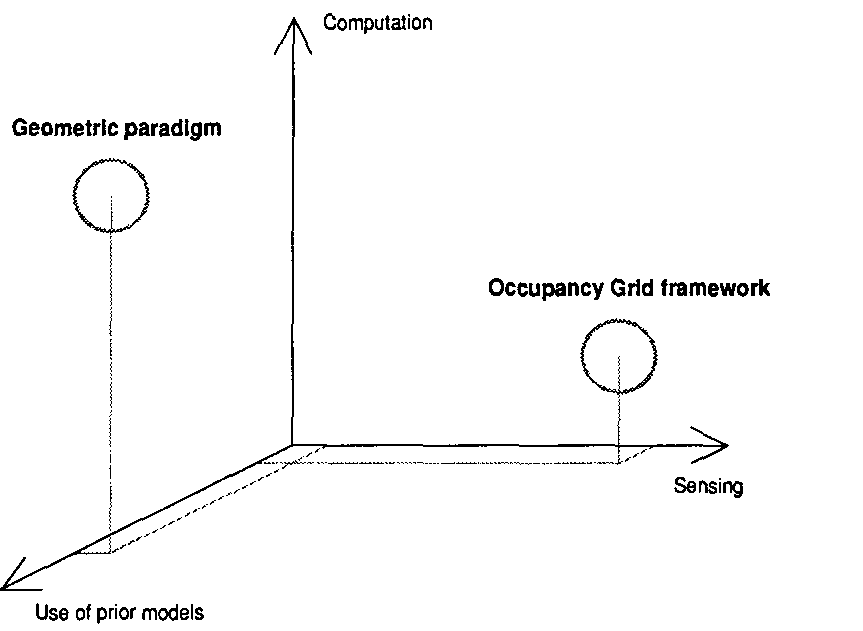
Figure 5. A comparison of emphases in the geometric paradigm versus the occu-
pancy grid framework.
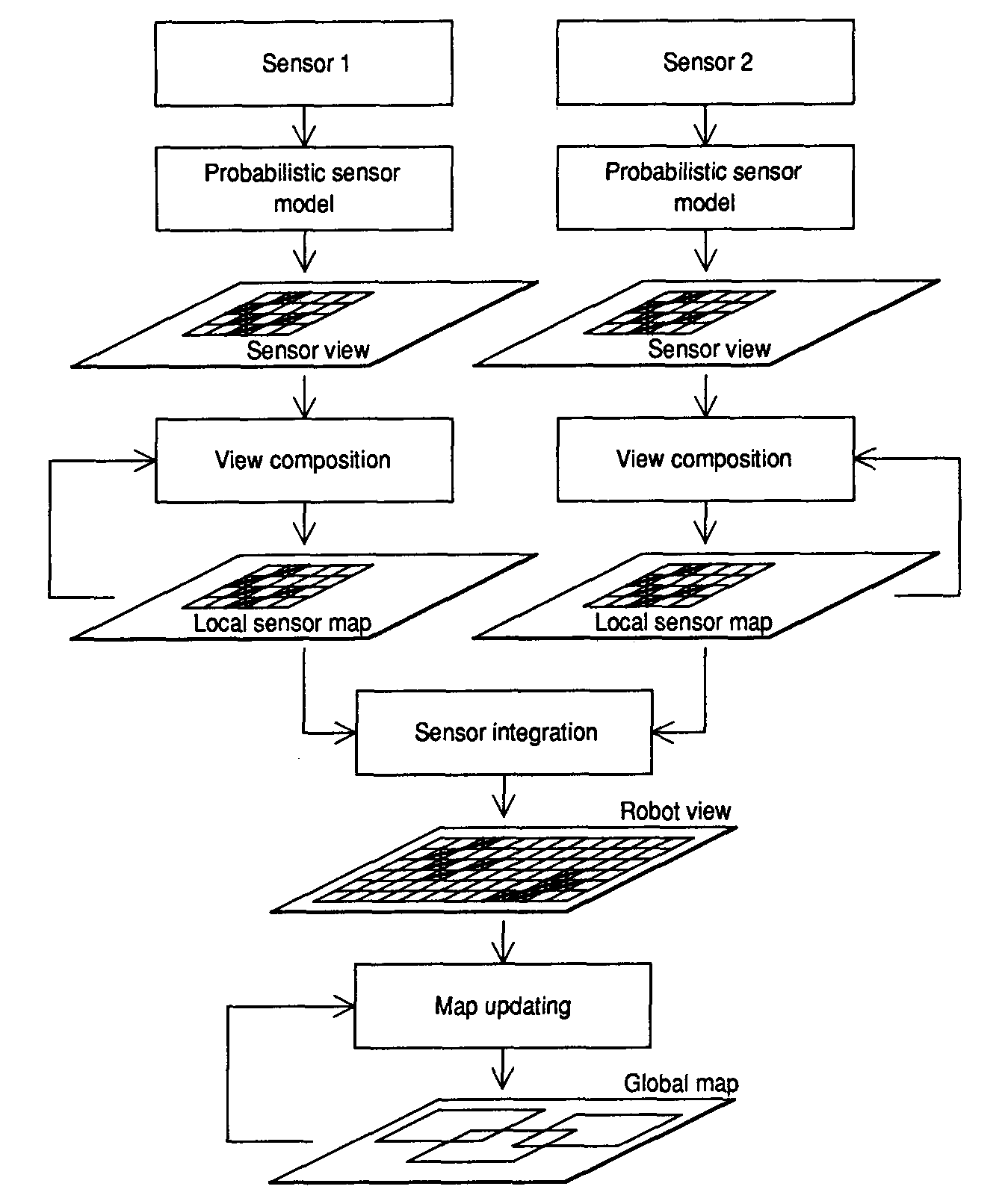
Figure 6. A framework for occupancy-grid-based robot mapping.
Using occupancy grids for
mobile robot mapping
Reviewing some applications to the
mobile robot domain will illustrate the
occupancy grid framework. This section
discusses the use of occupancy grids in
sensor-based robot mapping. The next
section provides an overview of their use
in robot navigation.
One possible flow of processing for the
use of occupancy grids in mobile robot
mapping appears in Figure 6. The vehicle
explores and maps its environment, ac-
quiring information about the world. Data
acquired from a single sensor reading is
called a sensor view. Various sensor views
taken from a single robot position can be
composed into a local sensor map. Mul-
tiple sensor maps can be maintained sepa-
rately for different sensor types, such as
sonar or laser. To obtain an integrated
description of the robot’s surroundings,
sensor fusion of the separate local sensor
maps is performed to yield a robot view,
which encapsulates the total sensor infor-
mation recovered from a single sensing
position. As the vehicle travels through its
terrain of operation, robot views taken
from multiple data-gathering locations are
composed into a global map of the envi-
ronment. This requires the registration of
the robot views to a common frame of
reference, an issue addressed in the next
section.
For experimental validation, the frame-
work outlined above was implemented and
tested on several mobile robots in both
indoor and outdoor scenarios. We will look
at some results derived from experiments
in sonar-based mapping and in sensor inte-
gration of sonar and single-scanline stereo.
Sonar-based mapping. Early work
with sonar-based mapping3,9 initially mo-
tivated the development of occupancy
grids and led to the implementation of a
mobile robot range-based mapping and
navigation system called Dolphin. A vari-
ety of experiments were used to test this
system.1,3 For indoor runs, a mobile robot
called Neptune was used (see Figure 7);
outdoor runs were performed with a larger
robot vehicle called the Terregator. More
recently, a new version of the Dolphin sys-
tem was installed on the Locomotion
Emulator, a mobile platform designed for
navigation in mining environments (see
Figure 8).

Figure 7. The Neptune mobile robot, built by Gregg Podnar at the Carnegie
Mellon University Mobile Robot Lab, shown with a circular sonar sensor array
and a pair of stereo cameras. Vehicle locomotion and sensor interfaces are con-
trolled by on-board processors, while the Dolphin mapping and navigation sys-
tem runs on an off-board mainframe. This robot was used for indoor range
mapping and sensor integration experiments.

Figure 8. The Locomotion Emulator mobile robot, built at the CMU Field Robot-
ics Center. Designed for navigation experiments in mining environments, this
vehicle is capable of implementing several locomotion strategies. It is shown here
with a sonar sensor array.
Figure 9 displays a typical 2D sonar
occupancy grid, while Figure 10 provides
a 3D plot of the corresponding occupancy
probabilities. Examples of other maps are
given in Figure 11, which shows a sonar map
obtained during navigation down a
corridor, and Figure 12, which corresponds
to a run in a wooded outdoor park.
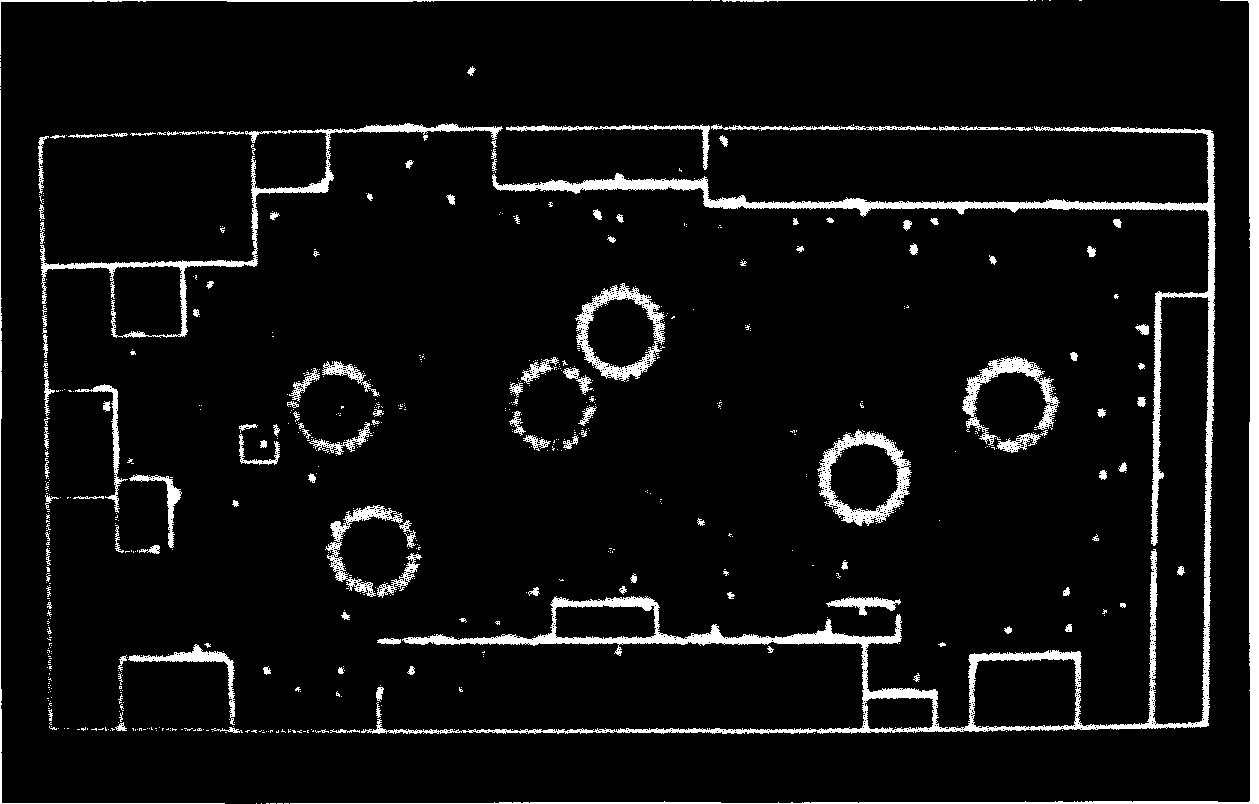
Figure 9. A two-dimensional sonar occupancy grid. Cells with high occupancy
probability are represented in red, while cells with low occupancy probability
are shown in blue. The robot positions from where scans were taken are shown
by green circles, while the outline of the room and of major objects is given by
white lines. This map shows the Mobile Robot Lab.

Figure 10. Occupancy grid probabili-
ties for the sonar map. This 3D view
shows the occupancy probabilities
P[s(Cxi yj) = OCC](xi, yj) of the map in
Figure 9.
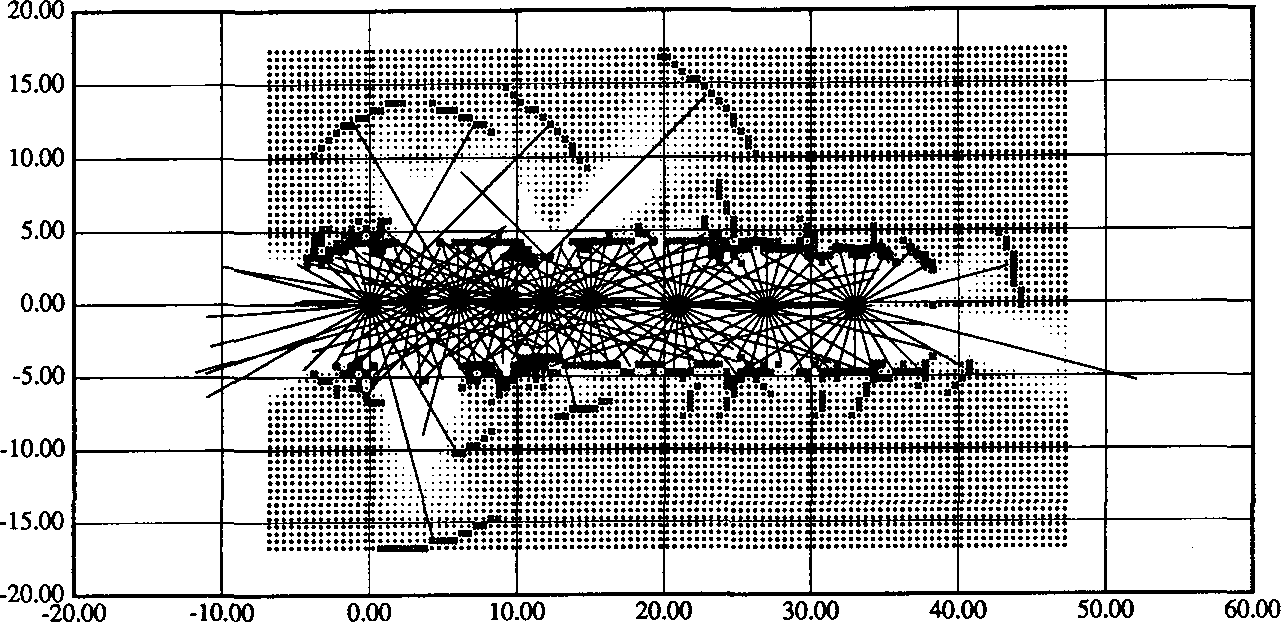
Figure 11. Sonar mapping and naviga-
tion along a corridor. Walls and open
doors can be distinguished, and the
resolution is sufficient to allow wall
niches to be noticeable in the map. The
range readings taken from each robot
stop are drawn superimposed on the
occupancy grid.
Sensor integration of sonar and scan-
line stereo. The occupancy grid frame-
work provides a straightforward approach
to sensor integration. Range measurements
from each sensor are converted directly to
the occupancy grid representation, where
data taken from multiple views and from
different sensors can be combined natu-
rally. Sensors are treated modularly, and
separate sensor maps can be maintained
concomitantly with integrated maps, al-
lowing independent or joint sensor opera-
tion. In collaboration with Larry Matthies,
I have performed experiments in the fusion
of data from two sensor systems: a sonar
sensor array and a single-scanline stereo
module that generates horizontal depth
profiles.4 For sensor integration runs, the
Neptune mobile robot was configured with
a sonar sensor ring and a pair of stereo
cameras (see Figure 7). The independent
opinion pool method, mentioned earlier,
was used to combine the occupancy grids
derived separately for the two sensor sys-
tems.
Figure 13 shows a typical set of maps. In
general terms, we can see that the inte-
grated maps take advantage of the comple-
mentarity of the sensors. The stereo system
depends on matching high-contrast image
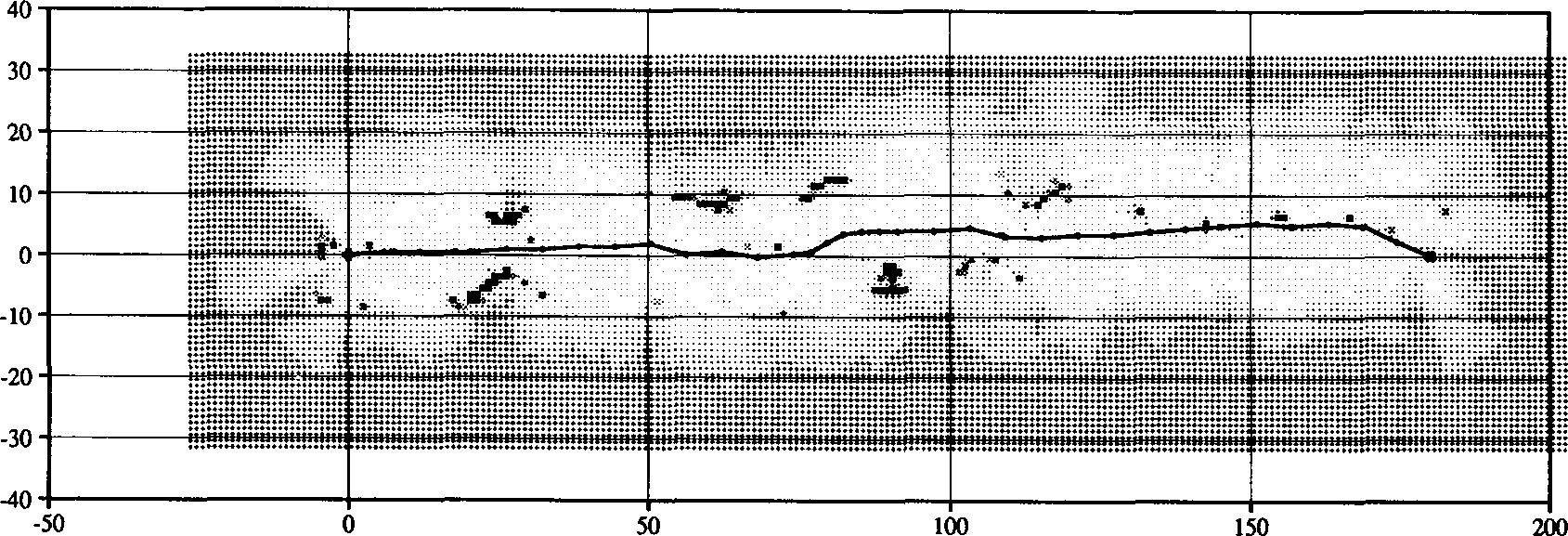
Figure 12. An outdoor run. This map shows a sonar-based outdoor run in a wooded park area. The obstacles encountered
are trees.
features, so unmarked surfaces or low-
contrast edges are not detected well. Stereo
angular resolution is comparatively high,
while the range uncertainty increases with
distance. Sonar, on the other hand, detects
surfaces well. But it has poor angular reso-
lution due to the large beam width, while
the range uncertainty itself is compara-
tively low. Some of these characteristics
become noticeable in Figure 13, where
sonar misses open paths due to its beam
width, while stereo misses object edges
due to low contrast against the background.
A corrective behavior can be seen in the
integrated map.
Using occupancy grids
for mobile robot
navigation
We now turn to some examples of the
use of occupancy grids in mobile robot
navigation. We briefly address issues in
path planning, estimating and updating the
robot position, and incorporating the posi-
tional uncertainty of the robot into the
mapping process (as shown in Figure 14).
Path planning. In the Dolphin system,
path planning and obstacle avoidance are
performed using potential functions and an
A* search algorithm. The latter operates
directly on the occupancy grid, optimizing
a path cost function that takes into account
both the distance to the goal and the occu-
pancy probabilities of the cells traversed.1,3
Results of the operation of the path planner
can be seen in Figures 11 and 12.
Handling robot position uncertainty.
To allow the merging into a coherent model
of the world of multiple views acquired by
the robot from different sensing positions,
we need accurate motion information to
allow precise registration of the views for
subsequent composition. For mobile ro-
bots that move around in unstructured
environments, recovering precise position
information poses major problems. Over
longer distances, dead reckoning estimates
are not sufficiently reliable. Consequently,
motion-solving methods that use landmark
tracking or map matching approaches are
usually applied to reduce the registration
imprecision due to motion. Additionally,
the positional error is compounded over
sequences of movements as the robot trav-
erses the environment. This leads to the
need for explicitly handling positional
uncertainty and taking it into account when
composing multiview sensor information.
To represent and update the robot posi-
tion as the vehicle explores the terrain, we
use the approximate transformation (AT)
framework developed by Smith, Self, and
Cheeseman.10 A robot motion M, defined
with respect to some coordinate frame, is
represented
as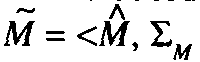 >, where
>, where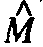 is
is
the estimated (nominal) position and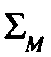 is
is
the associated covariance matrix that cap-
tures the positional
uncertainty. The para-
meters of the robot motion are determined
from dead reckoning and inertial
naviga-
tion estimates, which can be composed

Figure 13. Sensor integration of sonar
and scanline stereo. Occupancy grids
generated separately for sonar (a) and
scanline stereo (b), as well as the inte-
grated map (c) obtained through sen-
sor fusion, are shown. Occupied re-
gions are marked by shaded squares,
empty areas by dots fading to white
space, and unknown spaces by +
marks.
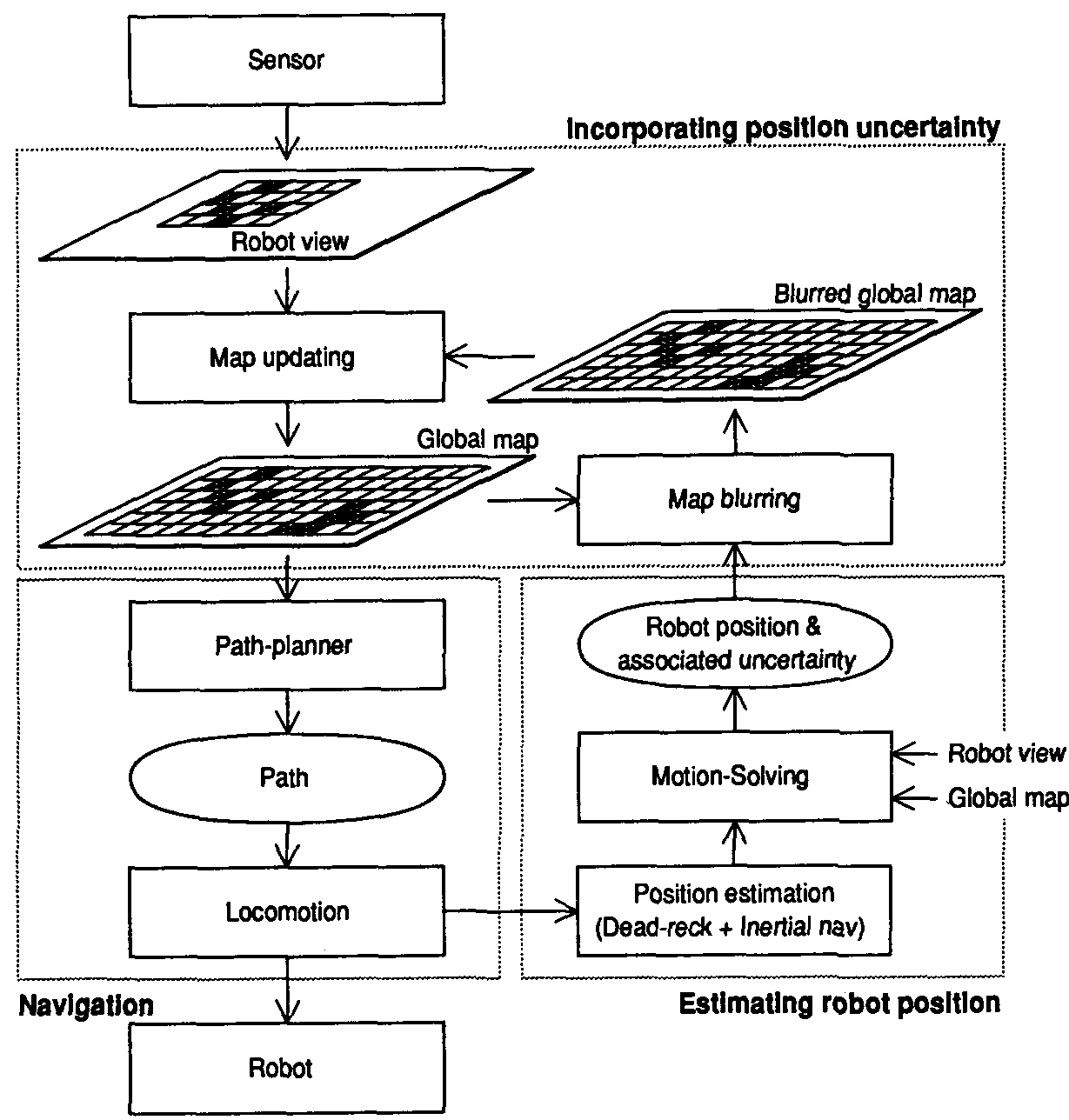
Figure 14. A framework for occupancy-grid-based robot navigation. New robot
views are used to update the global map, which in turn is used by the path plan-
ner. After locomotion, the new robot position estimate is refined using a motion-
solving procedure that finds an optimal registration between the robot view and
the current global map. Finally, the remaining positional uncertainty is incorpo-
rated into the map updating process as a blurring operation.
the composition of maps by the symbol 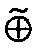 ,
,
the world-based mapping procedure can be
expressed as
global map <— global map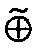 (robot
(robot
view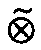 global
position uncertainty)
global
position uncertainty)
Since the global robot position uncer-
tainty increases with every move,
this
updating
procedure has the effect that the
new views become progressively more
blurred, adding less and less
useful
infor-
mation to the global map. Observations
seen at the beginning of the exploration are
“sharp,”
while recent observations are
“fuzzy.” From the point of view of the
inertial observer, the robot
eventually
“dissolves” in a cloud of probabilistic
smoke.
For robot-based mapping, we estimate
the registration uncertainty of the global
map due to the recent movement of
the
robot, and the global map is blurred by this
uncertainty prior to composition with the
current
robot view. This mapping proce-
dure can be expressed as
global map <— (global map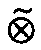 local
local
position uncertainty)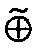 robot
view
robot
view
A consequence of this method is that
observations performed in the remote past
become
increasingly uncertain, while re-
cent observations have suffered little blur-
ring. From the point of
view of the robot,
the immediate surroundings (which are of
direct relevance to its current
navigational
tasks) are “sharp.” The robot is leaving, so
to speak, an expanding probabilistic
trail
of
weakening observations (see Figure 15).
Note, however, that the local spatial
relationships observed within a robot
view
still
hold. To avoid losing this information,
we use a two-level spatial representation,
incorporating
occupancy
grids and ap-
proximate transformations. On one level,
the individual views are stored attached
to
the
nodes of an AT graph (a stochastic
map10) that describes the
movements of the
robot. On the second level, a global map is
maintained that represents the robot’s
cur-
rent overall knowledge of the world (see
Figure 16). This two-level structure pro-
vides an
adequate and efficient representa-
tion for various navigation tasks.
Operations on
occupancy grids
We have looked at the application of the
occupancy grid framework to the mobile
using the AT merging operation, while the
updating of the robot position uncertainty
over several moves is done using the AT
composition operation.10
Motion solving. For more precise posi-
tion estimation, we employ a multiresolu-
tion correlation-based motion-solving pro-
cedure.9 Increasingly lower resolution
versions of the occupancy grids are gener-
ated, and the search for an optimal registra-
tion between the current robot view and the
global map is done first at a low level of
resolution. The result is subsequently
propagated up to guide the search process
at the next higher level of resolution.
Incorporating positional uncertainty
into the mapping process. After estimat-
ing the registration between the new robot
view and the current global map, we can
incorporate the associated uncertainty into
the map updating process as a blurring or
convolution operation performed on the
occupancy grid. We distinguish between
world-based mapping and robot-based
mapping.1,2 In world-based mapping, the
motion of the robot is related to an absolute
or world coordinate frame, and the current
robot view is blurred by the robot’s global
positional uncertainty prior to composi-
tion with the global map. If we represent
the blurring operation by the symbol and
and
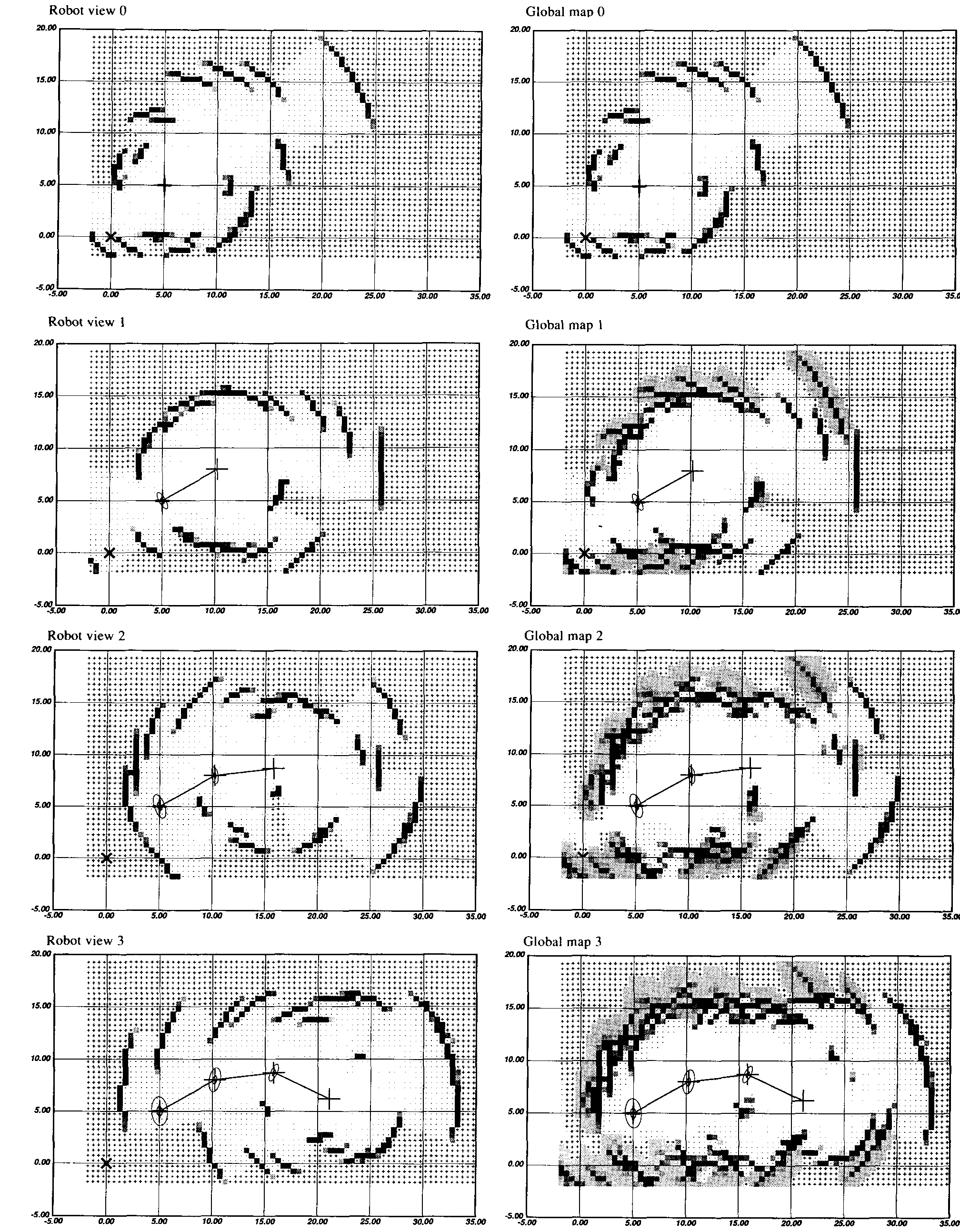
Figure 15. Incorporating motion uncertainty into the mapping process. For robot-centered mapping, the global map is
blurred by the back-propagated robot position uncertainty (shown using the corresponding covariance ellipses) prior to
composition with the robot view.
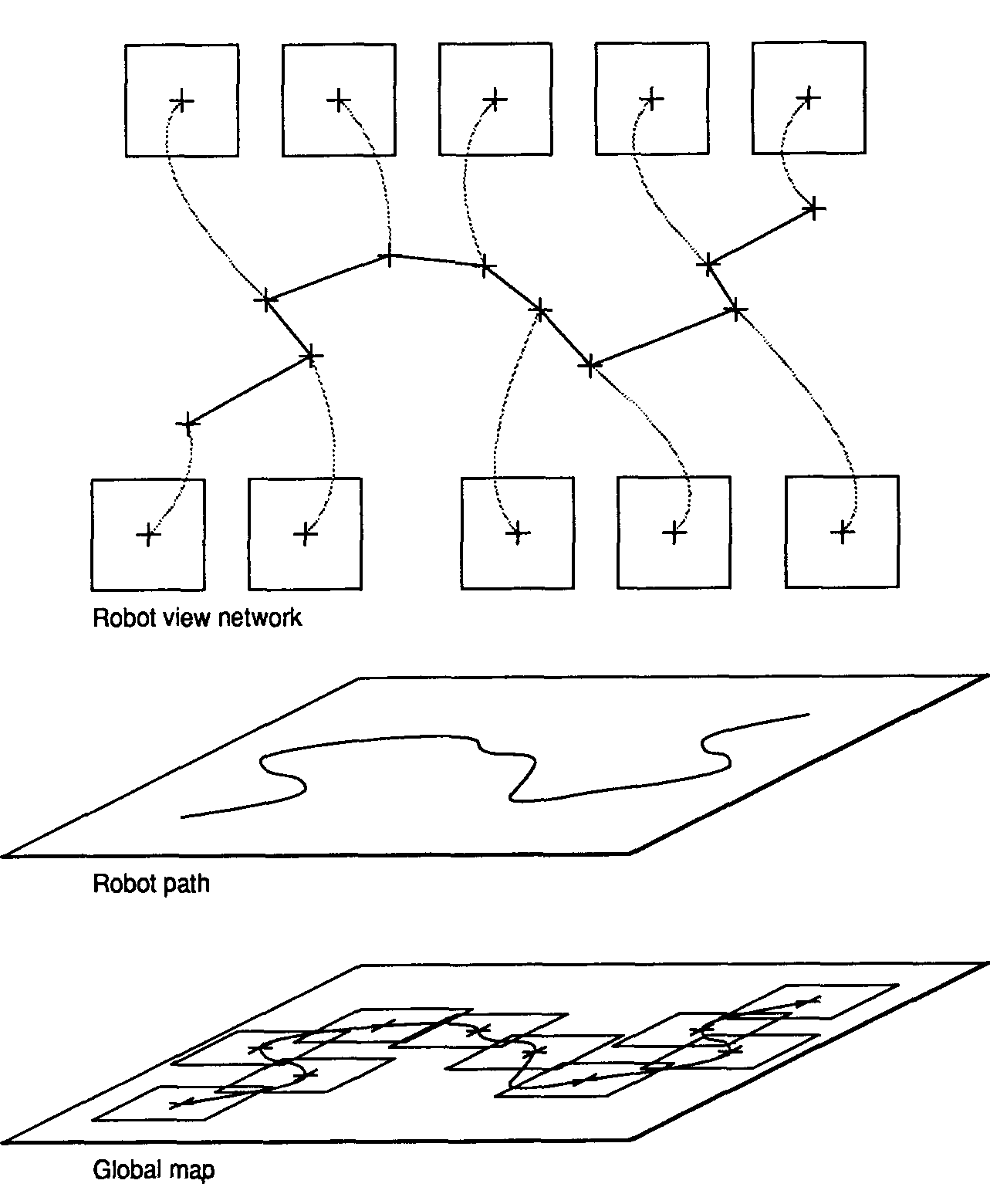
Figure 16. Maintaining a two-level spatial representation. The individual robot
views are stored attached to the nodes of an AT graph describing the robot mo-
tion and are maintained in conjunction with the global map .
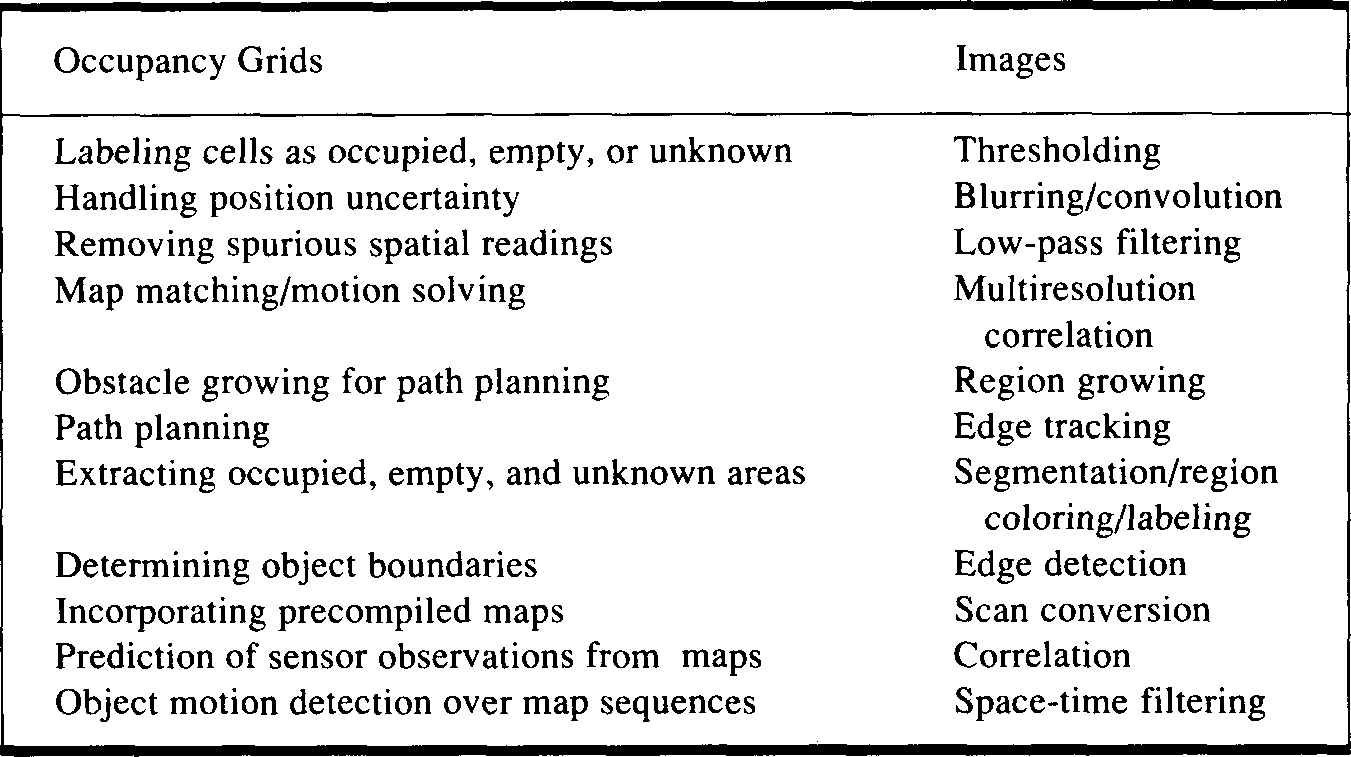
Table 1. Operations on occupancy grids for various robotic tasks and similar
operations performed in the image processing domain.
robot mapping and navigation domain.
This framework also allows us to address a
number of other robot perception and spa-
tial reasoning problems in a unified way. It
is important to observe that many opera-
tions performed on occupancy grids for
various robotic tasks are similar to compu-
tations performed in the image processing
domain. This is a useful insight, since it
allows us to take advantage of results from
this context. Table 1 provides a qualitative
overview and comparison of some of these
operations.
Extending the
occupancy grid
framework
Additional issues explored within the
occupancy grid framework include the
recovery of geometric descriptions from
occupancy grids,3 the incorporation of
precompiled maps,1 and the use of log-
arithmic maps where the resolution drops
with the distance to the robot.1 Other pos-
sible applications include the prediction of
sensor readings from occupancy grids and
the detection of moving objects over se-
quences of maps. Current work is investi-
gating other domains, such as the use of oc-
cupancy grids for laser scanner mapping,
precise positioning, and navigation in
mining applications using the Locomotion
Emulator; the development of mapping
and planning strategies that take advantage
of high-level precompiled maps when
available; the exploration of strategies for
landmark recognition and tracking; and
the recovery of 3D occupancy grids from
laser rangefinders or stereo depth profiles.
We have reviewed the occu-
pancy grid framework and
looked at results from its ap-
plication to mobile robot mapping and
navigation in unknown and unstructured
environments. The occupancy grid frame-
work represents a fundamental departure
from traditional approaches to robot per-
ception and spatial reasoning. It supports
agile and robust sensor interpretation
methods, incremental discovery proce-
dures, composition of information from
multiple sensors and over multiple posi-
tions of the robot, and explicit handling of
uncertainty. Furthermore, the occupancy
grid representation can be used directly in
various robotic planning and problem-
solving activities, thereby precluding the
need for the recovery of deterministic geo-
metric models. The results suggest that the
occupancy grid framework provides an ap-
proach to robot perception and spatial
reasoning that has the characteristics of
robustness and generality necessary for
real-world robotic applications.
Acknowledgments
The research discussed in this article was
performed when I was with the Mobile Robot
Lab, Robotics Institute, Carnegie Mellon Uni-
versity. I wish to acknowledge Hans Moravec
for his support and suggestions concerning this
work. I also wish to thank Peter Cheeseman,
Jose Moura, Larry Matthies, Radu Jasinschi,
Sarosh Talukdar, Art Sanderson, Michael
Meyer, and Larry Wasserman for their com-
ments concerning some of the issues discussed.
This research was supported in part by the
Office of Naval Research under Contract
N00014-81-K-0503. I was supported in part by
a graduate fellowship from the Conselho
Nacional de Desenvolvimento Cientifico e
Tecnologico, Brazil, under Grant 200.986-80;
in part by the Instituto Tecnologico de
Aeronautica, Brazil; and in part by the Mobile
Robot Lab, CMU.
The views and conclusions contained in this
document are my own and should not be inter-
preted as representing the official policies, ei-
ther expressed or implied, of the funding agen-
cies.
References
-
1. A. Elfes, Occupancy Grids: A Probabilistic
Framework for Mobile Robot Perception
and Navigation. PhD thesis. Electrical and
Computer Engineering Dept./Robotics
Inst., Carnegie Mellon Univ., 1989. -
2. A. Elfes, “A Tesselated Probabilistic Rep-
resentation for Spatial Robot Perception,”
Proc. 1989 NASA Conf, on Space Tele-
robotics, NASA/Jet Propulsion Labora-
tory, California Inst, of Technology, Pasad-
ena, Calif., Jan. 31-Feb. 2. 1989. -
3. A. Elfes, “Sonar-Based Real-World Map-
ping and Navigation," IEEE J. Robotics
and Automation. Vol. RA-3, No. 3, June
1987. -
4. A. Elfes and L.H. Matthies, “Sensor Inte-
gration for Robot Navigation: Combining
Sonar and Stereo Range Data in a Grid-
Based Representation,” Proc. 26th IEEE
Conf, on Decision and Control. Dec. 1987.
Also in Proc. 1988 IEEE Int'l Conf, on
Robotics and Automation, CS Press, Los
Alamitos, Calif. -
5. E. Vanmarcke, Random Fields: Analysis
and Synthesis. MIT Press, Cambridge.
Mass.. 1983.
-
6. J.O. Berger, Statistical Decision Theory
and Bayesian Analysis. 2nd ed.. Springer-
Verlag. Berlin. 1985. -
7. A.E. Bryson and Y.C. Ho, Applied Optimal
Control, Blaisdell Publishing. Waltham,
Mass., 1969. -
8. D.J. Kriegman. E. Triendl. and T.O. Bin-
ford. "A Mobile Robot: Sensing. Planning,
and Locomotion,” Proc. 1987 IEEE Int'l
Conf, on Robotics and Automation, CS
Press, Los Alamitos. Calif., April 1987. -
9. H.P. Moravec and A. Elfes. "High-Resolu-
tion Maps from Wide-Angle Sonar," Proc.
IEEE Int'l Conf, on Robotics and Automa-
tion, CS Press. Los Alamitos. Calif.. March
1985. -
10. R.C. Smith, M. Self, and P. Cheeseman, “A
Stochastic Map for Uncertain Spatial
Relationships,” Proc. 1987 Int'l Symp. on
Robotics Research. MIT Press, Cambridge,
Mass., 1987.

Alberto Elfes is a researcher with the Engi-
neering Design Research Center and the Robot-
ics Institute at Carnegie Mellon University. His
research interests include robotics, computer
vision, mobile robots, and design automation
systems. His current work addresses the devel-
opment of probabilistic and estimation theory
approaches to robot perception and spatial
modeling, and the use of spatial reasoning tech-
niques in design automation. He has published
more than 30 articles in these areas.
Elfes received the EE degree in electronics
engineering in 1975 and the MS degree in
computer science in 1980 from the Instituto
Tecnologico de Aeronautica, Brazil. He was
granted the PhD degree in 1989 by the Electri-
cal and Computer Engineering Department at
Carnegie Mellon University. He is a member of
the IEEE Computer Society, the IEEE, and the
ACM.
Readers may contact Elfes at the Robotics In-
stitute, Carnegie Mellon University, Pitts-
burgh, PA 15213.
NASA
Associate Chief
Space and Earth Science
Supercomputing Center
Goddard Space Flight Center is seeking candidates
for the position of Associate Chief NASA/Spacc and
Earth Sciences Supercomputing Center. The incumbent
will be responsible for planning, developing, and
managing the NASA large-scale scientific supercom-
puting facility. Additional responsibilities include
initiating programs generating advanced scientific com-
putational technology initiatives and acquislion of new
advance technology hardware configurations and
software systems.
Salary range ($57.158 to $74.303 per annum)
depending on education and experience. Applicants
must possess a B.S. degree in engineering, computer
science, mathematics, or the physical sciences and an
advanced degree or equivalent experience leading
research programs utilizing large-scale computing
hardware and software systems.
Candidates should submit a resume or Application
for Federal Employment (SF-171) to NASA/Goddard
Space Flight Center. Employment and Employee
Services Branch, Code 1 15 AC. Greenbelt. MD 20771.
Technical inquiries should be directed to Dr. Milton
Halem at (301) 286-8834. U.S. Citizenship is required.
Equal Opportunity Employer.
Programming
and Analysis
Supervisor
Information processing and communica-
tions laboratory is seeking computer
programmer to supervise programming
group. Responsible for: scheduling
programming and analysis tasks for
programmer analysts; actively seeking new
programming opportunities; supervising
user services function including documen-
tation review; programming and analysis
tasks in numerical analysis, real time
programming and/or statistics. Master’s in
related field or equivalent experience with
5 years professional supervisory ex-
perience required. Experience in FOR-
TRAN, C, and assembler language and
knowledge of calculus perferred. Apply to:
Personnel Manager
Box 54P

WOODS HOLE
OCEANOGRAPHIC
INSTITUTION
Woods Hole, MA 02543
An equal opportunity employer M/F/H/V
Elfes, A. Using Occupancy Grids for Mobile Robot Perception and Navigation / A. Elfes.– Text :
electronic // Computers. – 1989. – vol. 22, no. 6. – pp. 46-57. – URL:
https://www.researchgate.net/
publication/2953854_Using_Occupancy_Grids_for_Mobile_Robot_Perception_and_Navigation